|
||||||||||||||
|
Грант РФФИ «Разработка модели процессов формирования побеговых систем древесных растений на основе параметризации частично обратных матриц для представления кроны как мультимасштабной структуры» Номер проекта 16-04-01617 Руководитель — Антонова Ирина Сергеевна, кандидат биологических наук, доцент
На первый взгляд, мы знаем о дереве всё, и в нем нет ничего загадочного. Дерево состоит из ствола и ветвей, они, в свою очередь, бывают мелкие (веточки) и крупные (сучки). В популярных изданиях нередко попадаются изящные модели деревьев, построенные на основе графов. На экране компьютера в определённых программах они иногда даже колышутся под «порывами ветра». Всё здорово и красиво. Но если задуматься о сути того, что отражают эти модели, неизбежно возникает вопрос: насколько компьютерное ветвление соответствует биологическому процессу появления новой ветви? И тут оказывается, что эти модели не имеют никакого отношения к основам биологического ветвления. Кроме графов, модели дерева строятся на основе L-систем, натяжения (обертывания ветви сеткой на манер трубопровода) и других вариантов, применяемых в технике. Несомненно, для первичных результатов такие модели полезны и интересны. Но биологический процесс нуждается в существенно более тонком анализе. Лучшие ботанические атласы чаще всего характеризует форму кроны либо как поверхность определенной геометрической фигуры (шарообразная, цилиндрическая, конусовидная, и т.д.), либо как форма известного предмета, например зонтиковидная, яйцевидная, обратно-яйцевидная, либо как «крона неправильной формы», причем последнее определение встречается довольно часто. Глядя на рисунок ветвей, ботаник без труда определит род и часто даже вид листопадного дерева. Иначе говоря, человеческий глаз фиксирует особенности, присущие структуре кроны вида, но до сих пор остаются неясными даже основные принципы ботанического описания этих особенностей. Знание разнообразных свойств кроны дерева на практике необходимо для лесоведения, лесоводства, семеноводства и плодоводства. Оно позволит, например, рассчитывать урожайность плодовых деревьев, таких как персик, яблоня, грецкий орех и других. Кроме того, учет строения кроны необходим:
Для науки также имеют значение экологические и эволюционные особенности видов при их расселении по Земле, выживании в разные исторические периоды, так как вегетативное тело растения непосредственно соприкасается с окружающей средой, изменяется под ее действием и трансформирует эту среду, обеспечивая возможность существования и размножения организмов. Современная иностранная литература отражает большой интерес к этим проблемам в мире. Основоположниками западной школы исследования структуры кроны древесного растения стали Halle и Oldemann (1970). В крупных исследовательских центрах Франции, США, Канады, Японии и других стран проводится большое количество исследований структуры крон сельскохозяйственных плодовых деревьев с применением современных математических методов. Такие научные направления и целые школы возглавляют P. Prusinkiewicz, P.B. Tomlinson, H. Honda, Cl. Edelin, C. Godin, Y. Guédon, E. Costes, D. Barthelemy, Y. Caraglio. Интересно, что в русской ботанике вопросы строения кроны дерева рассматривались в рамках проблемы жизненных форм еще в 20-30-е годы прошлого века. Начиная с этого времени, создавались различные ответвления исследований форм травянистых и древесных растений в трудах Н.И. Вавилова, Н.П. Кренке, Т.А. Работнова, И.Г. Серебрякова, Т.И. Серебряковой, С.Я. Соколова, И.А. Грудзинской, В.К. Василевской, Ю.Л. Цельникер. Позже это направление продолжали и продолжают: Л.Е. Гацук, Л.М. Шафранова, О.В. Смирнова и их ученики и последователи. Представителями особой школы, связанной с изучением филлотаксиса и лесных сообществ, являются В.А. Брынцев и другие представители школы МГУЛ. Однако в связи с тем, что преобладающими жизненными формами на территории нашей страны являются травы и кустарники, именно им в настоящее время уделяется основное внимание исследователей. Это работы школы, сформировавшейся под руководством Серебряковых и Работного в МГПИ, мощное направление, разработанное под руководством Л.А. Жуковой и многих других. Исследования, посвящённые деревьям, теряются в основном потоке биоморфологических работ. Многолетние исследования строения крон растений Северо-Запада, средней России и Кавказа позволили нам сформулировать пятиуровневую иерархическую систему единиц строения крон листопадных растений умеренной зоны (Антонова И. С., Фатьянова Е. В. О системе уровней строения кроны деревьев умеренной зоны // Ботанический журнал. 2016, т. 101, № 6. Стр. 628-649., см. рис.1). 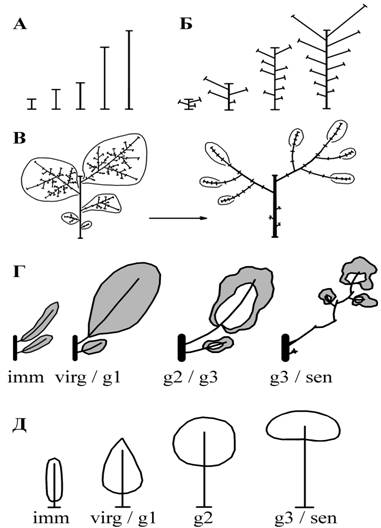 Рисунок 1. Схемы, отражающие уровни строения кроны дерева. А – уровень побега: разнообразие побегов кроны в выборках меняется плавно; Б – уровень двухлетних побеговых систем: в кроне присутствует небольшое количество типов (чаще 5–9), в выборках меняется дискретно; В – эпсионы (в виргинильном возрастном состоянии и в старом генеративном) в кроне присутствует небольшое количество типов; Г – ветвь от ствола (форма ветви изменяющаяся в различных возрастных состояний), в кроне присутствует небольшое количество типов; Д – крона дерева (в разных возрастных состояниях). В основе системы лежит анализ побегового состава растения на всех последовательных стадиях его онотогентичсекого развития. К общей известной всем характеристике побега наши исследования добавили следующие положения:
При этом предполагается, что окончательные свойства побег приобретает лишь на второй год своей жизни, когда раскрываются и вырастают его пазушные почки, тогда он приобретает особый, характерный для вида габитус. На основании наблюдения и анализа ветвей различных пород деревьев в определённых возрастных состояниях были выделены двулетние побеговые системы (ДПС) – следующий важнейший элемент строения кроны. На рис. 2 приведены 4 типа ДПС. Эти типы встречаются у всех исследованных нами 35 видов древесных растений, так как они выполняют функции построения скелета и скелета дерева и обрастания его мелкими ветвями, несущими основную массу листьев. 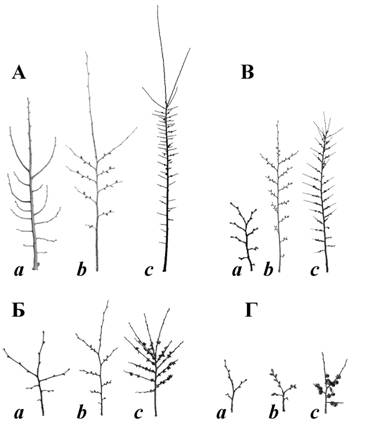 Рисунок 2. Базовое разнообразие двухлетних побеговых систем (ДПС). А – ростовые ДПС; Б – основные; В – узкоконтурные; Г – заполняющие пространство кроны (a – для Tilia cordata, b – для Ulmus laevis, c – для Diospyros lotus). Форма контура определенного типа ДПС – устойчивый признак вида (при условии выбора для сравнения систем сходного положения в системе кроны) (рис. 3). Последовательность ДПС определяет строение ветви.  Рисунок 3. Совмещение нескольких ДПС с разных деревьев Ulmus glabra. Показано полное совпадение формы ДПС Анализ материалов по структуре кроны для построения модели на основе параметризации частично обратных матриц потребовал создания целого комплекса программ, которые приведены ниже.
Вспомогательные программные продукты для исследования крон деревьев, созданные в 2016 году при поддержке гранта РФФИ 16-04-01617. 1. База данных ANTREES. 82 признака, 6 возрастных состояний, 38 деревьев и ветвей вида Acer negundo. Получено Свидетельство Российской Федерации о государственной регистрации базы данных №2016621088 «База данных морфологических характеристик побегов для восстановления пространственно-временной структуры кроны Acer negundo» (ANTREES). Правообладатель: Федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский государственный университет» (СПбГУ). Авторы: Антонова И.С., Барт В.А., Бодягина К.Б., Соколова О.С. Заявка № 2016620794 от 09 июня 2016 г. Дата государственной регистрации в Реестре баз данных Российской Федерации 09 августа 2016 г. (см. рис. 4). Опубликовано в Официальном бюллетене «Программы для ЭВМ. Базы данных. Топологии интегральных микросхем». Дата опубликования 20.09.2016, М.: ФИПС, №9(119), 2016, 20.09.2016.  Рисунок 4. Свидетельство о государственной регистрации базы данных № 2016621088. 2. Программа ввода данных. На входе программы (источник данных): рисунок дерева целиком или его части на тетрадном листе. На выходе: массив данных для статистической обработки (индивид – побег; файл MS Excel), c заполненными полями 47 признаков таблицы «База побегов» БД ANTREES для всех побегов дерева:
- двумерный граф в виде таблицы последовательных координат вершин на плоскости. Язык кода программы: C++. Видео 1. Интерфейс с фоновым рисунком. 3. Программа 2D-визуализации модели дерева. На входе программы: таблица последовательных координат вершин. На выходе: интерактивный рисунок двумерного графа дерева или его части. Язык кода программы: C++.
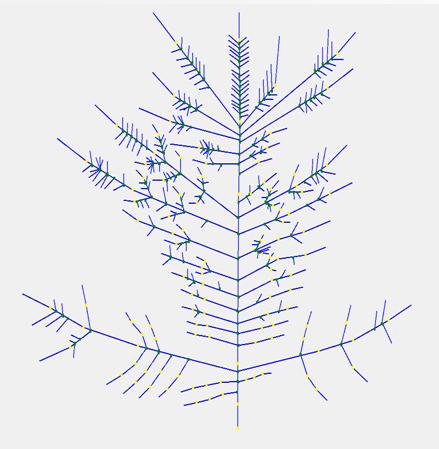 Рисунок 5. Интерфейс с рисунком 2D-графа. 4. Программа создания 3D-графа. На входе программы: массив данных таблицы «База побегов» для конкретного дерева базы БД ANTREES (файл MS Excel). На выходе: 3D-граф в виде таблицы последовательных трехмерных координат вершин (текстовый формат файла) для программы трехмерной визуализации. Язык кода: VBA. 5. Программа 3D-визуализации модели дерева. На входе программы: текстовый файл с последовательными координатами вершин 3D-графа «База побегов» для конкретного дерева базы БД ANTREES. На выходе: а) интерактивная панель с 3D-визуализацией модели дерева с возможностью вращения камеры в двух плоскостях, приближения-удаления; б) файл (*.avi) видеозаписи вращения модели дерева в горизонтальной плоскости. Язык кода: C++. Видео 2. 3D-манипуляции. Видео 3. 3D-вращение: реконструкция кроны отдельно стоящего дерева №27. Видео 4. 3D-вращение: крона дерева №26, измененная фитоценотическим влиянием. 6. Программа 3D-визуализации модели свободного роста дерева вида Acer negundo. На входе: меню параметров модели свободного роста. На выходе: файл (*.avi) видеозаписи вращения модели свободного роста дерева в горизонтальной плоскости. Язык кода: C++. Видео 5. 3D-вращение: модель свободного роста дерева Acer negundo (4 года). 7. Программа моделирования процесса типизации двулетних побеговых систем (ДПС). На входе программы: массив данных таблицы «База побегов» для конкретного дерева базы БД ANTREES (файл MS Excel). На выходе: таблица параметров всех ДПС дерева включая список их типов (файл MS Excel). (см. Антонова И.С., Барт В.А. Анализ метрических характеристик двулетних побеговых систем Acer negundo L. в молодом генеративном состоянии // Вестник Тверск. гос. ун-та. 2016. №4 (в печати)). Язык кода: VBA. 8. Программа DIGMA (двойного обобщенного обращения матриц). На входе программы: набор строк массива данных таблицы «База побегов» для конкретного дерева базы БД ANTREES (файл MS Excel), соответствующего конкретной ДПС. На выходе: Три 3D-графа в виде таблицы последовательных трехмерных координат вершин ДПС образа, прообраза и модели (текстовый формат файла) для программы трехмерной визуализации. Язык кода: VBA. Видео 6. 3D-вращение: пример 3D-модели образа, прообраза и реконструкции ДПС Acer negundo. Желтый цвет – образ, синий – прообраз, красный – модель. Реконструкция ДПС на основе двойного обобщенного обращения матриц Метод реконструкции ДПС основан на двойном обобщенном обращении матрицы (прямоугольной таблицы) А ее (ДПС) характеристик. Такая матрица строится на основе реально наблюдаемых метрических (морфологических) признаков ДПС. Такими признаками могут быть, например: длины междоузлий материнского побега, длины боковых побегов, углы ответвления боковых побегов и др. При этом шаг двойного обращения матрицы А соответствует формированию новой ДПС модели, которая строится по двойной обобщенно обратной матрице А--. Параметры однократного обобщенного обращения матрицы А, необходимые для получения матрицы А-, учитывают «внутренние» неморфологические (генетические, программные и т.п.) характеристики дерева на соответствующем пространственно-временном этапе ее формирования. Поэтому обобщенная обратная матрица А-, формируемая при однократном обращении, может интерпретироваться как носитель программной информации, передаваемой моделируемой ДПС и определяющей ее форму. Для построения частично обратных матриц А- и А-- для структурных матриц ДПС была написана компьютерная программа DIGMA на языке VBA (Microsoft Office, 2003). Для алгоритма построения были модифицированы рекурсивные формулы (Барт, Щербакова, 2007), а также коэффициент гамма (Барт и др., 2003) в качестве меры близости матриц образа и модели. На рисунке 6 приведены метрические характеристики двух ДПС дерева №27, полученные в результате запроса к базе данных ANTREES. В них вошли: длины междоузлий материнского побега и соответствующие им длины боковых побегов. По ним были построены матрицы А и В (см. рисунок там же), а также определены параметры двойного обобщенного обращения матрицы А и В, в данном случае – векторы коэффициентов альфа и бета – количества листьев на соответствующих боковых побегах. В предварительном морфологическом исследовании (Антонова, Гниловская, 2013) A. negundo было установлено, что длина боковых побегов ДПС слабо связана с количеством листьев на них. 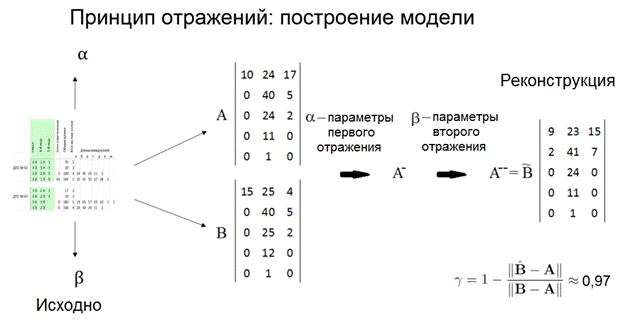 Рисунок 6. Схема алгоритма построения модели ДПС методом двойного матричного обращения. Коэффициент гамма всегда меньше единицы и равен ей только при полном совпадении матриц модели и образа. Полученный результат гамма 0,97 означает неплохое согласование модели и образа. Это говорит, прежде всего, о том, что выбранные параметры обращения «улавливают» различия между выбранными ДПС. Построение статистических оценок параметров и совместных доверительных областей распределения междоузлий на побеге В статье Антоновой и Барта (Вестник Тверского университета, январь 2016) была исследована модель многомерного нормального распределения для описания совместного расположения последовательных сумм длин крайних междоузлий побега A. negundo. Модель позволила вычислить границы совместных доверительных интервалов для четырех верхних и четырех нижних крайних узлов побега в зависимости всего от одного параметра – значения первой главной компоненты. С помощью модели впервые показана и исследована структура жесткого (программного) закрепления узлов верхней и нижней частей побега в отличие от более экологически подвижных средних узлов междоузлий. В зависимости от значений первой главной компоненты на побеге построены оценки максимального правдоподобия условных средних координат узлов на побеге. Исследование двулетних побеговых систем и их типизация на видах рода Acer В статье Антонова И.С., Барт В.А. (Вестник Тверского университета, декабрь 2016) «Анализ метрических характеристик двулетних побеговых систем A. negundo L. в молодом генеративном состоянии» описан алгоритм решающего правила типизации (как способ разбиения множества ДПС по типам). Разделение ДПС A. negundo на типы описывается с большой точностью линейными комбинациями пяти метрических признаков, также получено описание по более сложному правилу, но уже только двумя признаками. Тот факт, что все получаемые типы ДПС кодируются только двумя метрическими признаками, говорит о большой строгости программы развития и жесткости связей всех участвующих характеристик. 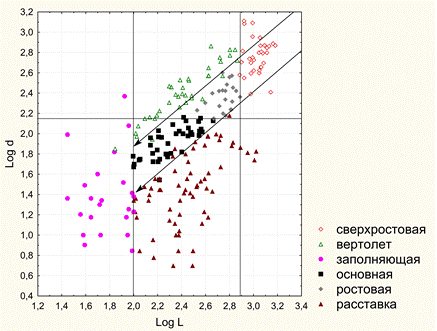 Рисунок 7. Решающее правило типизации ДПС A. negundo L. в молодом генеративном состоянии. По статистическому анализу ДПС других четырех видов этого рода опубликована статья Антоновой, Барта и Клочьковой в АПНИ (г. Белгород, декабрь 2016). В структуре кроны выявлены и типизированы двулетние побеговые системы (ДПС). Причем из них три типа идентичны по основным метрическим параметрам, а остальные четыре имеют характерные особенности. Построено решающее правило (рис. 8), моделирующее проведенную типизацию всего по двум метрическим признакам ДПС. Статья является продолжением серии работ авторов по модульному изучению морфологии кроны рода. 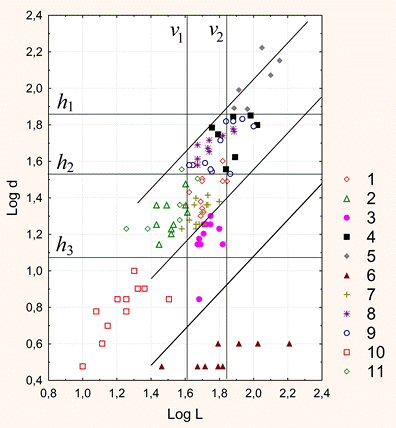 Рисунок. 8. Совместная диаграмма рассеяния признаков длины материнского побега L и максимальной длины d бокового побега ДПС 4 видов рода Acer (данные представлены в логарифмической шкале (длины измерены в мм)). Определение линий см. в тексте. 1 – ростовая (A. platanoides), 2 – основная (A. platanoides), 3 – узкоконтурная 1 (A. platanoides), 4 – кронообразующая (A. tegmentosum), 5 – суховершинная (A. tegmentosum), 6 – узкоконтурная 2 (A. tegmentosum), 7 – ростовая (A. cissifolium), 8 – кронообразующая (A. cissifolium), 9 – кронообразующая (A. henryi), Aзаполняющая (A. henryi), 11 – основная (A. henryi).
В 2017 году созданы следующие компьютерные программы. а) Запрос к базе данных ANTREES на представление списка всех ДПС выбранного дерева в форме просмотра. Результат работы программы необходим при выделении и отборе ДПС по значениям основных морфологических признаков. На входе: номер дерева БД ANTREES. На выходе: книга MS Excel со списком всех ДПС дерева в виде «побег-строка» упорядоченными по коду материнского побега. Язык кода программы: MS VBA.
б) Запрос к базе данных ANTREES на представление списка всех ДПС выбранного дерева в виде «строка – ДПС». Для применения статистических процедур, построения графиков необходимо представление ДПС как индивида (Case) в применяемом статистическом анализе. На входе: номер дерева БД ANTREES. На выходе: лист MS Excel с упорядоченным списком ДПС дерева в виде «строка – ДПС» со следующими характеристиками:
Язык кода программы: MS VBA.
в) Запрос к базе данных ANTREES на представление списка всех ДПС выбранного дерева в виде «ДПС – матрица» для выбора и подстановки в программу DIGMA (отчет за 2016 год). На входе: номер дерева БД ANTREES, количество боковых побегов, количество междоузлий на материнском побеге. На выходе: лист MS Excel c последовательностью ДПС по вертикали в матричной форме, нули заменены на единицы. В последовательность входят только те ДПС, параметры которых не меньше запрошенных. Язык кода программы: MS VBA.
г) Запрос к базе данных ANTREES на перекодировку побегов дерева с «верхней» на «нижнюю». Верхняя и нижняя кодировки побега и их применение на практике подробно описаны в статье (Антонова И.С., Барт В.А. Строение крон древесных растений умеренной зоны на примере Acer negundo L. и Ulmus glabra Huds, 2017). На входе: номер дерева БД ANTREES, возраст дерева. На выходе: лист MS Excel c последовательностью всех побегов дерева с номером побега на дереве и кодами двух типов в трех первых столбцах. Язык кода программы: MS VBA.
д) Программа параллельного вращения структурных единиц кроны. Эта программа необходима для визуального сравнения моделей реальных деревьев, 3D-реконструкции кроны, подготовки презентаций, проч. Основная причина: двумерные рисунки деревьев как основная форма собранных данных для БД ANTREES не содержит всей информации о расположении и направлении роста побегов дерева в пространстве. При параллельном сравнении разных крон или близких участков одной кроны выявляются необходимые поправки к поворотам осей побегов в пространстве. Вращение 3D-моделей есть наилучший способ их визуализации на двумерном экране. Программа пригодна также для сравнения метрических характеристик ДПС, эпсионов, ветвей, и решения вопросов, связанных с симуляцией геометрического контура ДПС и определения его типа. На входе: книга MS Excel с упорядоченным списком ДПС дерева в виде «строка – ДПС» со следующими характеристиками:
На выходе: панель параллельного вращения выбранных ПС (Видео 1.2017). Видео 1.2017. Интерфейс программы параллельного вращения. Язык кода программы: C#.
е) Запрос к БД ANTREES на вход программы параллельного вращения. На входе: номер левого дерева БД ANTREES, номер правого дерева БД ANTREES. На выходе: книга MS Excel с упорядоченным списком ДПС деревьев в виде «строка – ДПС» со следующими характеристиками:
Язык кода программы: MS VBA.
Дальнейшее изучение строения кроны дерева показало его жесткую структурную иерархию пространственно-временных структурных единиц, подчинённых друг другу: побег, двулетняя побеговая система (ДПС), эпсион, ветвь от ствола, крона. Эти единицы управляют развитием единиц нижнего по отношению к себе уровня. Из них основными являются ДПС и крона. На изменение внешних факторов программа развития дерева реагирует в основном изменением своего состава по типам основным структурным единиц, и почти не меняет их морфологические характеристики внутри каждого типа. Так, показано, что в отличие от длины побегов при сравнении деревьев разных местообитаний тип ДПС остается тем же. Это соответствует принципам А.А. Любищева о целостности систем организма: единство целого при разнообразии частей. Построена модель зональности побега, определяющая его классификацию как структурной единицы кроны. Это совершенно новая пространственно-временная классификация, индуцированная ДПС, а для ростовых побегов – и структурными единицами более высокого уровня. Это значит, что для мелких побегов управление их ростом происходит на двулетнем уровне, тогда как для крупных ростовых побегов это управление выходит на уровень многолетних побеговых систем. Изменение метрических характеристик побега связано с программным недоразвитием целых зон на нем, причем последнее определяется более высоким уровнем иерархии. Построена модель кривых продолжительности роста макропобега, связывающая пространственно-временные свойства побега и кроны. Модель позволяет по-новому подойти к решению задач идентификации и сравнения побегов и ДПС, учитывая построенную структурную зональность побега. Так же она пригодна для учета зональности при биологически обоснованном выборе параметров при 3D-реконструкции кроны. На основе двух выборок по 100 единиц каждая удалось построить общую модель геометрического контура ростовой и основной ДПС Ulmus glabra. Структурная зональность материнского побега ДПС двух типов рассматривается как естественное обобщение модели экспоненциального роста. В статье была выделена зона из трех первых междоузлий, характеристическая для ДПС ростового типа. Был проведён сбор материала по побеговым системам видов р. Quercus L, интродуцированных в Абхазии. За две поездки были собраны 2-4-летние ветви данных видов в количестве: Q. acuta – 13 ветвей, в них – 179 побегов, Q. glauca – 30 ветвей, 319 побегов, Q. myrsinaefolia – 36 ветвей, 521 побег. В октябре 2017 г во время поездки во Владивосток был собран материал по побеговым системам Betula schmidtii Regel – 20 деревьев. Все данные в настоящее время занесены в электронные таблицы и готовы для дальнейшей обработки в БД «ANTREES». Продолжен набор данных в расширение БД «ANTREES»: введено 150 побегов Acer negundo, 100 деревьев U. glabra, более 11 деревьев Q. acuta и Q. glauca: 17 деревьев. Создано 6 компьютерных программ и запросов к БД «ANTREES». С помощью этих программ отобраны деревья и модель кривых продолжительности роста макропобега. Изучена литература на основе чего сформулированы четыре биологических принципа, которые позволяют создать базу для построения моделей архитектуры кроны: принцип отражений, принцип основной программы развития структурной единицы, принцип задержки развития как единственной альтернативы смерти, принцип зеркальности начала и конца роста побега. Отданы в печать 4 статьи, сделаны 4 доклада на 2 международных конференциях, в 4 печатных работах опубликовано их содержание.
В 2018 выполнено... 1. Реконструкция ДПС по выборке Betula schmidtii Regel. Сборы материала по березе B. schmidtii проводились в Дальневосточном морском государственном заповеднике. На опушке вторичного леса, расположенного на мелкосопочнике близ бухты Витязь в октябре 2017 года, были выбраны генеративные особи с диаметром стволов 12–15 мм. Из освещенной нижней части кроны одинаковой экспозиции были выбраны верхушки осей второго порядка в возрасте от 2 до 5 лет. Для всех ветвей составлены подробные схемы с указанием количества побегов, типа побегов (удлиненный или укороченный) года образования и угла ответвления, а также длин междоузлий, количества листьев и присутствия генеративных органов. Всего изучено 165 ДПС. Кроме того, собраны три трехлетние верхушки дерева и генеративные ветки 5 и 6 лет. ДПС отличаются по общему количеству листьев на оси, по порядку ветвления оси. Особенности строения побеговых систем позволяют выделить три типа ДПС: «ростовые», «основные» и «заполняющие». Более подробное описание выборки приведено в (Кременецкая, Антонова, 2018). Все ДПС боковых ветвей имели плагиотропный рост, плоскостное расположение в пространстве и не имели силлептических побегов. Так же, как и в случае U. glabra, описанном в статье (Антонова, Барт, 2018, Белгород), матрица прообраза по выборке B. schmidtii была составлена из медиан длин междоузлий и длин соответствующих им боковых побегов. Отличие состояло в том, что для всех типов ДПС исходный прообраз оценивался по наиболее многочисленной группе «основных» ДПС.
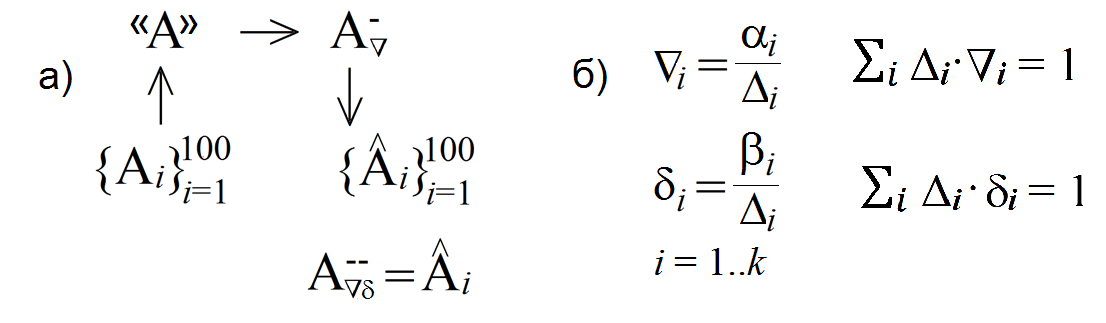 Рисунок 2018.1. а) Схема реконструкции ДПС вяза и березы Шмидта по выборке; Ai – матрица некоторой ДПС; «A» – исходный прообраз ДПС, оцененной по выборке; б) Формулы построения компонент векторов параметров обращения матриц по параметрам модели α и β и два условия дополняющей нежесткости; Δi – i-ый минор матрицы А при их лексикографическом упорядочивании; ∇i, δi – компоненты векторов параметров обращения матриц.
В таблице 2018.1 приведены результаты реконструкции выбранной ДПС «основного» типа по ее выборке. В первых столбцах представлены матрицы исходного прообраза «A», вектора ее параметров α, оцененные по выборке всех «основных» ДПС, и исходной матрицы B построенной по некоторой выбранной нами «основной» ДПС выборки. Ее элементы – это значения первых 6-ти междоузлий от верхушки материнского побега длин ДПС. Вектор параметров, состоящий из количества листьев на каждом из боковых исходной матрицы, по коэффициентам которой конструируется модель А-- =
Таблица 2018.1. Результаты реконструкции выбранной ДПС «основного» типа B. schmidtii по соответствующей ей выборке.
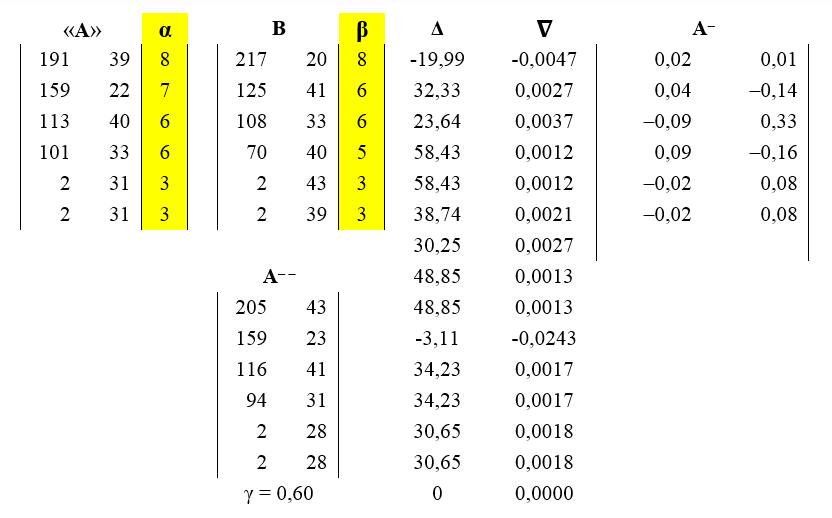
На рисунке 2018.2 представлены визуализации выбранной ДПС и ее модели.
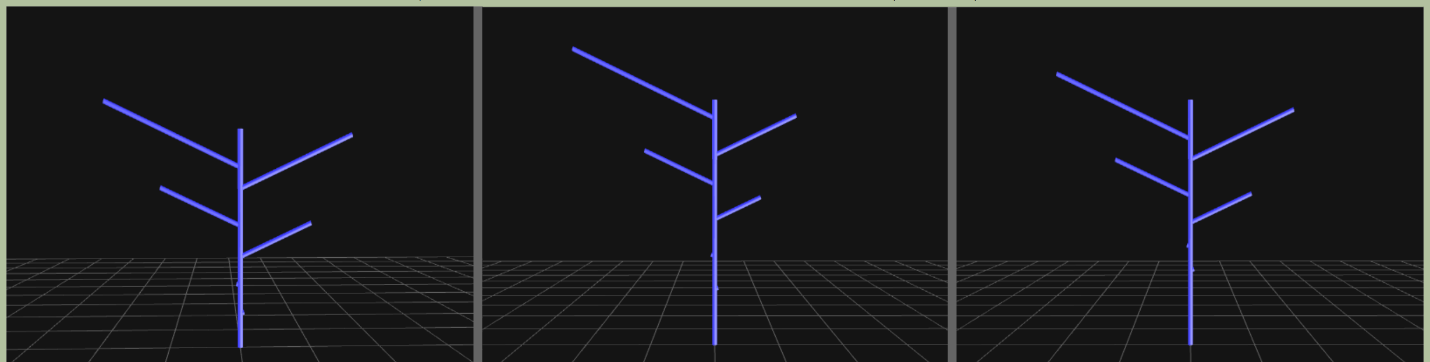 Рисунок 2018.2. Последовательно: прообраз (матрица «А»), 3D-реконструкция реальной выбранной конкретной «основной» ДПС B. smidtii (матрица B, первых 6-ти междоузлий от верхушки материнского побега) и ее модель (матрица А--). Все матрицы и параметры соответствуют таблице 2018.1.
В отличие от моделей, построенных по клену и вязу, в модели B. schmidtii признаки количества листьев на боковых побегах, выбранные в качестве параметров обращения, имели низкую вариабельность. Это приводило к эффекту, при котором все построенные модели мало отличались от оценки исходного прообраза. С биологической точки зрения это означает прежде всего то, что для B. schmidtii значительно отличается от других видов берез отсутствием массового силлептического роста побегов, сжатым периодом роста побегов, а также настолько плотной древесиной, что получило название «железное дерево». Вероятно, эти качества приводят к очень жесткой программной структуре боковых побегов.
2. Технические детали и компьютерное сопровождение. Стандартный массив признаков «База побегов» базы данных БД ANTREES дополнен тремя признаками:
Написан и отлажен код для программ-запросов к обновленной БД ANTREES. При этом учитывался способ представления исходной матрицы Ai и матрицы прообраза «А». При разрежении матриц нулями в шахматном порядке компоненты вектора параметров Δ интерпретируется как площади секторов, определяемых боковыми побегами и соответствующими им междоузлиями (рис. 3а). При обычном, последовательном, расположении длин междоузлий в матрице компоненты Δ эквивалентны разностям соседних площадей (рис. 3б).
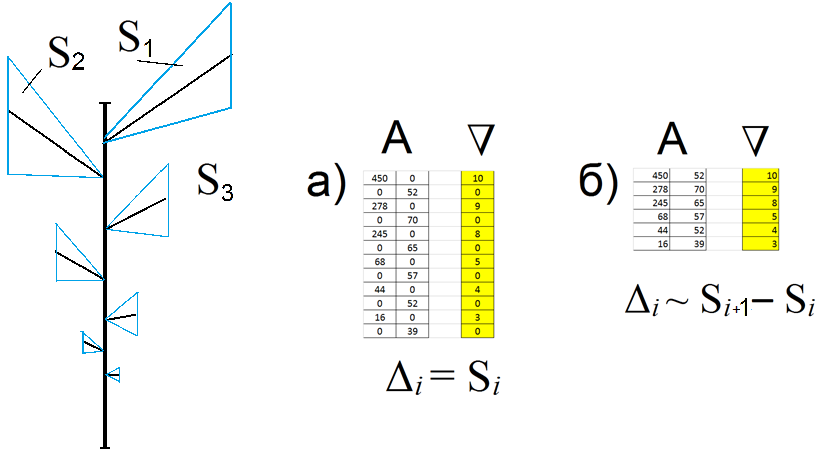 Рисунок 2018.3. Примеры представления ДПС матрицей с разрядкой нулями и без нее.
Программы: 1-2) Запрос к тестовым массивам для реконструкции частичным обращением по выборке (построение исходной матрицы «А», прореженной нулями и непрореженной исходной матрицы – 2 программы). На входе программы: массив данных таблицы «База побегов» для конкретного дерева базы БД ANTREES (файл MS Excel). На выходе: Матрица оценки компонент «А» и упорядоченный набор матриц первого и второго обращений «А» и их параметров для всех матриц ДПС выборки (файл MS Excel). Язык кода: VBA.
3-4) Запрос для реконструкции частичным обращением индивидуальной матрицы (прореженной нулями и без прореживания – 2 программы). На входе программы: массив данных таблицы «База побегов» для конкретного дерева базы БД ANTREES (файл MS Excel). На выходе: Матрица выбранной исходной ДПС В и прообраза А и упорядоченный набор матриц первого и второго обращений А и их параметров (файл MS Excel). Язык кода: VBA.
5-6) Программа многократного обращения исходной матрицы с постоянными параметрами (с нулями и без – 2 программы). На входе программы: массив данных таблицы «База побегов» для конкретного дерева базы БД ANTREES (файл MS Excel), номер материнского побега, количество двойных обращений. На выходе: упорядоченный набор матриц многократного двойного обращения А и их параметров (файл MS Excel). Язык кода: VBA.
Дополнение к БД ANTREES (новые признаки и запросы) позволяют единообразно для нескольких видов деревьев (A.negundo, U.glabra, Q.myrsinifolia, Betula smidtii, Ulmus parvifolia, Ulmus minor, Ulmus и других) формировать исходные матрицы и векторы параметров для реконструкции.
Конференции: 1. Современные проблемы биоморфологии, Владивосток, 3–9 октября 2017 г. Антонова И.С., Барт В.А. Некоторые итоги изучения строения крон древесных растений умеренной зоны// В сб.: Биоморфологические исследования на современном этапе. Материалы конференции с международным участием: «Современные проблемы биоморфологии, Владивосток, 3-9 октября 2017г». Владивосток, Мор. гос. ун-т. 2017. С. 7–9. Зайцева Ю.В., Антонова И.С. Структурная организация побеговых систем Tilia cordata Mill. // В сб.: Биоморфологические исследования на современном этапе Материалы конференции с международным участием: «Современные проблемы биоморфологии, Владивосток, 3-9 октября 2017г». Владивосток, Мор. гос. ун-т. 2017. С. 75–77. 2. Биоразнообразие: подходы к изучению и сохранению. Антонова И.С., Барт В.А. Пространственно-временные отношения при развитии побеговых систем деревьеы умеренной зоны // Материалы международной научной конференции: «Биоразнообразие: подходы к изучению и сохранению. Тверь. 8–11 ноября 2017года.», Тверь, Твер. гос. ун-т, С. 21–24. Барт В.А., Антонова И.С. Новые подходы к моделированию развития побеговых систем деревьев умеренной зоны // Материалы международной научной конференции: «Биоразнообразие: подходы к изучению и сохранению. Тверь. 8–11 ноября 2017 года.», Тверь, Твер. гос. ун-т, С. 31–32.
Статьи: Антонова И.С., Барт В.А. О целостности двулетних побеговых систем подроста Ulmus glabra Huds. // Бот. журн. 2018. (в печати). Антонова И.С., Барт В.А. Особенности двулетней побеговой системы и побегов подроста Ulmus glabra Huds. в связи с положением на осях разных порядков в трех типах лесных сообществ // Бот. журн. 2018. (в печати). Антонова И.С., Попова А.С. О морфологии почечных чешуй и катафиллов Ulmus glabra Huds. (Ulmaceae) // Тр. по прикладной ботанике, генетике и селекции, 2018. (в печати). Антонова И.С., Барт В.А. Строение крон древесных растений умеренной зоны на примере Acer negundo L. и Ulmus glabra Huds // Бюл. БСИ ДВО РАН (в печати).
Список работ:
|
|||||||||||||





